RÉELS (NOMBRES)

RÉELS (NOMBRES)

Par les différents adjectifs généralement accolés au substantif commun qu’est le nombre, la langue mathématique familière surprend et inquiète, car elle risque de susciter des confusions: nombres rationnels (d’autres nombres seraient donc sans raison?), nombres réels (des nombres doués d’existence propre?), nombres algébriques (seuls susceptibles des règles de l’algèbre ?), nombres transfigurés, nombres hyperréels, nombres cardinaux, nombres flous, etc.

L’histoire, naturellement, explique cette richesse du vocabulaire. Elle justifie l’organisation des adjectifs par couples opposés, oppositions dont la constitution scande les conquêtes mathématiques sur le champ numérique. Nombres réels et nombres imaginaires forment un couple antagoniste, de même que le couple nombres rationnels – nombres irrationnels, ou encore le couple nombres algébriques – nombres transcendants. Cette histoire embrasse l’évolution générale des mathématiques, tout particulièrement pour ce qui concerne les nombres qualifiés de réels. En effet, on peut sans exagération en faire remonter la théorie à la Grèce classique, la Grèce d’Euclide, celle de la génération d’après Alexandre le Grand. Pourtant, la construction mathématique des nombres réels ne fut réglée que vers les années 1870, élaborant la révolution de la théorie des ensembles, laquelle a débouché tant sur la topologie, dont la formalisation est de notre siècle, que sur la logique. Bien des propriétés fines de l’ensemble des nombres réels sont de découverte contemporaine. De même, le problème antique de la quadrature du cercle ne connut de solution négative qu’en 1882, et ce malgré une mutiplicité d’approches. Cette multiplicité même conduisit l’Académie royale des sciences de Paris, en 1776, à ne plus accepter l’examen de prétendues solutions positives. La structure algébrique de l’ensemble des nombres réels ne fut explicitée qu’après l’invention des quaternions en 1843. Enfin, un avatar de modèles logiques conduisit à l’analyse non standard vers les années 1960, fournissant un nouveau regard sur les nombres réels, un regard qui redonne de l’actualité à des idées mises en avant par Leibniz lors de la fondation du calcul différentiel. Le parcours historique est donc considérable.

En outre, cette histoire déborde largement le cadre mathématique car, avec ce qu’il est convenu aujourd’hui d’appeler nombres réels, on touche fondamentalement aux idées concernant le continu, le temps, donc l’atomisme ou la division à l’infini. Sur de tels thèmes, la plupart des philosophes occidentaux de tous les siècles ont tenté des explications, avancé des systèmes. Il est alors impossible de ne pas évoquer des arguments qui, de Zénon à Einstein en passant par Pascal, Kant ou Bergson, jalonnent la conquête purement mathématique, quand bien même celle-ci les aurait comme gommés.

Dès Euclide, un ensemble de référence fut trouvé qui permit la comparaison des grandeurs, véritable paradigme philosophique du continu. Cet ensemble composé de rapports, de raisons, contient en particulier les rapports d’entiers, les nombres rationnels, mais n’était pas muni de structures aussi nettes que celles que forment l’addition et la multiplication sur les entiers. Ces entiers constituent, quant à eux, le paradigme du discret. Qu’il faille préciser cet ensemble de référence par un principe de maximalité est une découverte de la fin du XIX^e siècle. Elle fit scandale, mais permit enfin de mettre l’analyse mathématique sur ses pieds par constitution d’une référence universelle, l’ensemble des nombres réels. Le continu, d’un coup, s’élargissait. La construction de cet ensemble continu à partir des seuls nombres entiers, l’arithmétisme, obligea à repenser l’existence des êtres mathématiques et rendit caducs les essais intérieurs, tel le géométrisme cartésien. A l’intérieur même de l’ensemble de référence, les classifications débutèrent très tôt – les problèmes antiques en témoignent. Elles s’affinèrent de Diophante à la Renaissance, en passant par les Indiens et les Arabes, à partir du thème des solutions d’équations polynomiales. C’est l’algébrisme qui était porteur, numérisant l’ensemble de référence (multiplication et addition) mais introduisant, au XVII^e siècle, une troisième opération, l’exponentiation. La classification en nombres algébriques et nombres transcendants s’en déduisait ainsi que l’opposition entre nombres réels et nombres imaginaires. Au XX^e siècle, les trois grandes structures de l’ensemble des nombres réels furent bien individualisées: la structure d’ordre, la structure algébrique de corps, la structure topologique. Chacune, avec ses moyens propres d’investigation, donnait naissance à des espaces abstraits. Du coup, l’ensemble des nombres réels apparaît comme une particularisation, un sous-ensemble d’ensembles plus vastes. Le vocabulaire mathématique prend acte, par oppositions, de cette particularisation.

Cet article suit, grosso modo, l’ordre chronologique. Pourtant, afin de couvrir l’essentiel de la lente domestication du champ numérique, et pour éviter des retours en arrière dont fourmille l’histoire, nous nous permettrons quelquefois de poursuivre jusqu’à nos jours tel point de vue structurel, pour revenir ensuite à la chronologie un instant abandonnée.

1. Rapports et mesures des grandeurs

La mesure des longueurs

Dès qu’il s’agit de mesurer, une longueur par exemple, l’idée première est de la comparer avec une autre longueur, qui sert de référence, à laquelle on donne volontiers le nom d’«unité». Cette unité choisie (en fonction du type de longueur mesurée), on la reporte plusieurs fois de façon à recouvrir la longueur à mesurer. Si l’on tombe juste, le nombre entier de reports effectués constitue une mesure (relative donc) de la longueur; sinon, on doit se contenter de dire que cette mesure se situe entre tel nombre entier et son successeur. Pour préciser, il faut changer d’unité de référence. Une seconde idée est alors de prendre une partie exacte de l’unité initiale et de recommencer l’opération; dans bien des cas, on trouve une mesure sinon exacte, du moins qui paraît satisfaisante, et la mesure de la longueur initiale se présente de manière naturelle comme un rapport d’entiers. Se pose alors la question théorique de savoir si, une unité étant choisie, toute longueur peut ainsi se mesurer comme un quotient d’entiers. La réponse négative à cette question a sans doute constitué la première crise intellectuelle de l’humanité, car elle établissait par la seule raison démonstrative, une incohérence du sens commun.

Nous ignorons les circonstances exactes de cette démonstration, élaborée vers le VI^e siècle avant J.-C. dans le cadre de l’Ecole de Pythagore mais le témoignage d’Aristote, certes tardif, nous montre à l’œuvre une parfaite maîtrise du raisonnement par l’absurde. Comparons en effet la longueur de la diagonale d’un carré à celle d’un côté prise pour unité de référence. Si cette mesure est un quotient d’entiers, disons p/q, le théorème de Pythagore fournit aussitôt la relation (p/q )² = 2. La contradiction s’établit alors en établissant que les entiers p et q sont simultanément pairs et impairs. On peut en effet supposer l’un pair et l’autre impair, quitte à diviser chacun par un multiple convenable de 2, ce qui ne change pas le rapport. Comme un carré d’entiers n’est pair que si le nombre entier lui-même est pair, l’égalité p ² = 2q ² implique la parité de p soit p = 2r , où r est un entier; il en résulte la relation 2r ² = q ² d’où résulte, de la même façon, la parité de q.

Puisque la mesure de la diagonale par rapport au côté n’est pas exprimable comme rapport d’entiers, on la déclara inassignable, imprononçable (en grec 見福福兀精礼﨟), voire sans raison ( 見凞礼塚礼﨟), car on appelait «raison» (礼塚礼﨟) un rapport d’entiers, la logistique étant le calcul sur les entiers et les rapports d’entiers. La crise des irrationnels débutait.

Bien vite, d’autres mesures irrationnelles font leur apparition et Platon, dans le Théètète tente un premier essai de classification. La contradiction rencontrée dans la notion de mesure rendait-elle cette idée caduque ? On doit vraisemblablement à Eudoxe de Cnide ^{[cf. EUDOXE DE CNIDE]} le dépassement de la contradiction au prix d’un incroyable effort d’abstraction; faute de pouvoir calculer l’impensable mesure de la diagonale, Eudoxe pense l’incalculable. Sa théorie nous est connue à travers le livre V des Éléments d’Euclide et il n’est pas possible de rendre compte de l’histoire des nombres réels sans rentrer dans quelques détails de ce livre.

Les raisons

Le but cherché est de pouvoir parler de la raison de deux longueurs, cette raison étant perçue comme un outil de comparaison de ces deux longueurs, outil qui ne saurait se réduire à un rapport d’entiers. Eudoxe va donc ajouter d’autres rapports aux seuls rapports entiers par des encadrements habiles. De façon précise, il part de deux longueurs notées A et B et deux autres notées C et D. La notion clé est l’égalité entre la raison de A à B et la raison de C à D. Il y a égalité lorsque, quels que soient les entiers naturels positifs m et n, l’ordre de m A par rapport à n B est exactement le même que l’ordre de m C par rapport à n D. Autrement dit, on doit avoir les implications suivantes, où 礪 signifie «strictement plus grand»:

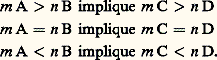Cette égalité des raisons, dont la transitivité est explicitement démontrée, permet aussitôt de parler de longueurs proportionnelles où la langue grecque, avec une remarquable économie de moyens, utilise le mot 見益見凞礼塚礼益, c’est-à-dire «longueurs analogues ayant même raison». L’étape suivante est de comparer les raisons (礼塚礼晴), en disant que si l’on a m A 礪 n B et m C 麗 n D pour deux entiers m et n , alors la raison de A à B dépasse la raison de C à D.

En particulier, lorsque m A = n B, tout autre couple de grandeurs proportionnelles C, D vérifie m C = n D et il paraît naturel d’attribuer à la raison commune la valeur m/n , rapport d’entiers. Ainsi, on évalue bien l’extension du domaine numérique réalisée par Eudoxe: les rapports d’entiers sont des cas particuliers de raisons. Notre langage contemporain porte encore la trace de cette assimilation puisqu’il qualifie ces rapports d’entiers de nombres rationnels. Mais les raisons qui ne se réduisent pas à des rapports d’entiers n’en sont pas moins des raisons, même si on les qualifie aujourd’hui de nombres irrationnels. Eudoxe ne commet pas cette étrange pétition de langage car il n’assimile pas une raison (礼塚礼﨟) à un nombre, c’est-à-dire un nombre entier ( 見福晴猪礼﨟). Cette attitude demande une explication. De fait, on peut combiner les nombres, entiers ou rationnels pour employer le langage actuel, au moyen de deux opérations, l’addition et la multiplication: on sait par exemple ce que sont 3 + 8 ou 3 憐 8 voire 25 + 13 ou 25 憐 13. Par contre, l’addition de deux raisons n’est jamais définie chez Euclide et la multiplication, définie seulement dans le cas de raisons égales, prend un autre nom (sous la forme du seul résultat, raisons dites «composées»). Autrement dit, le champ numérique n’a pas été étendu au domaine des raisons avec toutes ses propriétés opératoires; par contre l’ordre a été étendu, et tel était bien le but puisque l’idée de mesure est le motif de cette extension.

On peut transposer la construction précédente à d’autres grandeurs comme les aires, les volumes, les temps, les poids, les capacités ou les vitesses. Eudoxe et Euclide ont bien vu cette similarité d’approche et nous ont, en fait, fourni une théorie générale des raisons de grandeurs – pas de toutes les grandeurs imaginables, mais de celles susceptibles de raisons. Naturellement, dans notre pratique mathématique contemporaine nous aimerions dire que les mathématiciens grecs ont délimité une famille de grandeurs, puis, dans cette famille, axiomatisé la notion de mesure les conduisant à la définition des raisons. Une telle expression de la démarche d’Eudoxe, si elle n’est pas trop éloignée de la vérité, taille des habits trop étroits car trop précis. Il est bien vrai que les grandeurs en jeu sont avant tout celles susceptibles de comparaison, d’addition et de division par un entier. Ces trois outils ne sont d’ailleurs pas considérés indépendamment les uns des autres, comme notre habitude de la théorie des ensembles pourrait nous le faire induire. Deux grandeurs de même espèce (c’est-à-dire homogènes 猪﨎塚﨎諸益 礼猪礼塚﨎益諸益) sont comparables: soit égales, soit l’une dépassant strictement l’autre. En langage moderne, l’ordre est total. Mais deux grandeurs, A et B, toujours de même espèce, peuvent s’additionner et, en outre A + B 礪 A, ce qui traduit l’énoncé rhétorique: le tout est plus grand que la partie. Si, d’ailleurs, on a A 礪 B, il existe une grandeur de même espèce C telle que B + C = A. Enfin, les grandeurs sont divisibles, c’est-à-dire que, étant donné une grandeur A et un entier n, il existe une grandeur B telle que n B = A. Ainsi sont écartés du domaine des grandeurs susceptibles de raisons les nombres entiers, qui sont bien comparables et peuvent s’additionner, mais ne peuvent pas toujours se diviser par un entier en donnant un autre entier. Mais ce n’est pas tout; une propriété supplémentaire est requise: deux grandeurs auront une raison si, par multiplication convenable par des entiers, elles peuvent se dépasser mutuellement. Autrement dit A et B étant donnés avec A 麗 B, il est possible de trouver un entier n de telle sorte que:

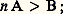on donne le nom d’Eudoxe-Archimède à cette propriété, car elle figure explicitement dans le livre V d’Euclide, partiellement attribué à Eudoxe, et le grand Syracusain en a souligné l’importance. Là encore cette restriction élimine certaines grandeurs. L’éradication la plus notable est celle des angles, que le Moyen Âge qualifiera de corniculaire, c’est-à-dire l’angle qu’une courbe fait avec sa tangente, par exemple l’angle déterminé entre un cercle et une perpendiculaire au rayon (partie hachurée sur la figure 1). En effet, Euclide établit, dans la proposition 16 du livre III, que cet angle corniculaire est plus petit que tout angle aigu de la forme BAC, et il est clair que tout sous-multiple de l’angle BAC est un angle aigu analogue. L’impossibilité de parler de la raison de l’angle corniculaire avec un angle aigu aura des conséquences épistémologiques lointaines au XVII^e siècle quand il s’agira de comparer des infiniments petits, c’est-à-dire de les mesurer. En disant que l’angle BAC est un infiniment petit du premier ordre lorsque B tend vers A le long du cercle et que l’angle corniculaire est, lui, du second ordre, on introduisit une notion d’ordre non archimédienne et on rompt avec la tradition euclidienne. Il faudra plus d’un siècle pour venir à bout de ce renversement. Et seule l’analyse non standard formalisera ce type de situation (cf. infra ).

Mais revenons à Eudoxe, en respectant ses limitations quant aux grandeurs concernées. Deux grandeurs homogènes entre elles peuvent avoir la même raison que deux autres grandeurs homogènes entre elles, mais non homogènes aux deux premières. Ainsi, on peut parler de la raison de la longueur de la circonférence d’un cercle à son diamètre et en dire l’égalité à la raison de l’aire de ce cercle au carré de son rayon. Non seulement en dire l’égalité, mais aussi la démontrer, comme le fait Archimède dans son court traité De la mesure du cercle.

Un modèle universel

Comme le domaine des grandeurs redevables du traitement d’Eudoxe est extensif, et non pas limitatif au sens de la théorie des ensembles – car il n’y a pas réduction à une espèce homogène de grandeurs –, le champ possible des raisons paraît très vaste, en tout cas aussi extensif que celui des grandeurs en jeu. Pourtant, et dès l’Antiquité, les mathématiciens ont paru restreindre ce champ et l’ont fait selon une intuition heureuse, mais qu’il fut très difficile de mettre ultérieurement en évidence. Essentiellement le domaine des raisons qu’il est possible de considérer pour des grandeurs comme les longueurs constitue tout le champ des raisons possibles. Ainsi, les raisons provenant de la comparaison des surfaces ou des volumes peuvent s’obtenir comme raisons déduites de la comparaison des seules longueurs. Autrement dit, le modèle construit à partir des longueurs est universel et peut servir pour la comparaison (par raisons) des poids, des capacités, des temps, etc. Entendu en ce sens universel, le domaine constitué par les raisons de longueurs (géométriques, rectilignes ou circulaires) joue pour les mathématiciens grecs le rôle que joue pour nous l’ensemble des nombres réels (positifs).

Il faut cependant prendre garde au fait que ce domaine des raisons de longueurs n’est absolument pas structuré, du moins du point de vue des opérations, comme les entiers et, a fortiori, comme notre corps des nombres réels. Nous avons vu que les raisons étaient ordonnées – l’ordre étant d’ailleurs total –, mais ni l’addition ni la multiplication n’y sont disponibles en toute généralité. Cependant ce domaine des raisons de longueurs est loin d’être inerte: certaines opérations y agissent et, sans trop forcer les termes, on peut prétendre qu’une algèbre y est ébauchée.

C’est d’ailleurs pour constituer les règles de manipulation de cette algèbre que se succèdent les propositions au cours du livre V. Donnons quelques exemples. D’abord un vocabulaire: dans une raison, celle de la grandeur A à la grandeur B, A est appelé l’antécédent et B le conséquent; à partir d’une proportion formée de quatre grandeurs prises dans cet ordre, où A est à B comme C est à D on introduit deux autres raisons, dites par permutation , celle de A à C et celle de B à D; ou deux autres raisons, dites par composition, celle de A + B à B et celle de C + D. On montre alors que ces diverses raisons sont égales. Au cours des siècles, ces règles deviennent autonomes et sont repérées, dans la tradition latine, par un vocabulaire descriptif: règle alternando règle componendo, règle separando, etc. Mais, pendant des siècles, aucune notation ne vient abréger l’énoncé des règles en proposant un graphisme qui en trivialise l’emploi, ne serait-ce que du point de vue mnémotechnique. Au XVII^e siècle, par exemple, et tard dans le XIX^e, on utilise pour désigner une proportion la notation suivante, qui est au mieux une écriture ordonnée:

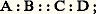avec cette écriture, les règles précédentes n’ont pas de visualisation évidente. On peut s’étonner d’un tel manque d’imagination chez les mathématiciens, d’habitude plus prompts, et limiter par cette remarque le début d’algébrisation constaté. On doit surtout, sur le plan épistémologique, souligner le rôle quelquefois majeur d’une notation ^{[cf. NOTATION MATHÉMATIQUE]}. Il semble que ce soit le Grand Arnauld qui, dans la troisième édition de sa Géométrie, destinée aux Petites Écoles de Port-Royal, a popularisé, pour désigner une proportion, la notation par barres de fractions, qui visualise bien les règles:

Quelques auteurs, comme A. De Morgan et, de nos jours, N. Bourbaki, ont voulu voir dans le domaine des raisons un domaine d’opérateurs agissant sur les grandeurs concernées: la raison de A à B, que l’on note A/B, agit sur la grandeur D afin de donner une grandeur C telle que A, B; C, D soit une proportion. L’idée est séduisante, car elle expliquerait l’intuition d’universalité du seul domaine des raisons de longueur, en identifiant entre eux tous les domaines d’opérateurs définis par toute espèce de grandeur. En outre, cette interprétation fait jouer un rôle très net à la règle de la quatrième proportionnelle. Cette règle énonce que, trois grandeurs étant données, A et B homogènes formant la raison A/B et D, il existe une quatrième grandeur C, de même espèce que D, telle que AB = CD . Cette règle est utilisée au livre V et plus encore au livre XII, où son intervention est cruciale pour le calcul de certaines aires. Pourtant, au livre V, la règle n’est jamais énoncée explicitement. Bien entendu, pour les longueurs, cette règle de la quatrième proportionnelle n’est autre que le théorème de Thalès. Portons en effet (fig. 2) sur une droite issue de O les longueurs A et B puis, sur une autre droite passant également par O, la longueur C. La quatrième proportionnelle se lit en C, à l’intersection de la droite OD et de la parallèle menée par A à la droite BD. Chez Euclide, le théorème de Thalès est énoncé dans la proposition 2 du livre VI.

Des calculs numériques

Cette puissante théorie des proportions ne se contente pas de satisfaire un esprit épris de définitions ayant belle ordonnance ou un amateur de règles de calcul un peu exotiques. Elle est aussi le moteur de calculs approchés et, en quelque sorte, récupère tout un courant logisticien développé avec brio par les Égyptiens et les Babyloniens. Cet aspect calculatoire fonctionne grâce à l’ordre sur les raisons, et, en utilisant des raisons particulières, les raisons de nombre à nombre, c’est-à-dire ce qu’il est convenu d’appeler les nombres rationnels. On encadrera donc entre deux nombres rationnels une raison que l’on cherche à estimer. C’est ainsi qu’Archimède donne l’encadrement fameux:

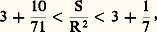où la raison S/R² est celle de l’aire S d’un cercle au carré de son rayon. Depuis Euler, on note ce nombre 神, et la majoration de droite fournit la fraction bien connue 22/7.

Cette méthode d’encadrement des raisons est une des méthodes les plus raffinées qui aient été mises au point par la mathématique grecque. Grégoire de Saint-Vincent au XVII^e siècle, lui a donné le nom de «méthode d’exhaustion». On la trouve pour la première fois à l’œuvre dans le livre XII d’Euclide. Cependant, chez Euclide, l’aspect numérique est totalement occulté, soit par préjugé philosophique d’origine platonicienne, soit par souci didactique, soit encore par refus de fournir des résultats n’ayant pas encore atteint le dernier poli requis. Nous suivrons plutôt Archimède et l’articulation de la méthode d’exhaustion en trois temps à l’occasion de son calcul de S/R² (pour le rôle de la méthode d’exhaustion, cf. l’article histoire du CALCUL INFINITÉSIMAL). Archimède établit d’abord l’égalité de S/R² avec p /d , où p désigne le périmètre du cercle et d son diamètre.

1^er temps: mise en place d’un raisonnement par l’absurde. Soit S l’aire du cercle et soit T l’aire du triangle rectangle dont un côté de l’angle droit a pour longueur le rayon du cercle et l’autre pour longueur le périmètre du cercle. La démonstration de l’égalité des raisons p/d et S/R² revient à établir l’égalité des aires S et T. L’idée est alors de montrer que l’inégalité stricte S 礪 T est impossible, de même que l’inégalité stricte S 麗 T.

2^e temps: mise en place d’un processus algorithmique de dichotomie avec un jeu quasiment algébrique sur les proportions. Par exemple, pour établir que l’inégalité S 礪 T est impossible, Archimède inscrit un carré dans le cercle, puis divise en deux chaque arc sous-tendu, obtenant un octogone. Il renouvelle ensuite l’opération de dichotomie. Une estimation est alors faite à chaque étape de ce qui manque pour que l’aire de la figure polygonale fournisse l’aire du cercle. Or il est possible de montrer que, dans le passage du carré à l’octogone, on gagne plus que la moitié de l’aire qui manque au carré pour donner l’aire du cercle et que chaque dichotomie réalise un gain semblable. L’axiome d’Eudoxe-Archimède permet alors sans peine de montrer que, au bout d’un nombre suffisant d’étapes de la dichotomie, la différence entre l’aire polygonale et l’aire du cercle est inférieure à une quantité donnée à l’avance. Le choix de cette quantité préassignée est alors celui de la différence présupposée entre l’aire S et l’aire T. On en déduit que l’aire polygonale à laquelle s’est arrêtée la dichotomie est plus grande que l’aire T. Pourtant, l’aire de cette figure polygonale est celle d’un triangle rectangle dont un côté de l’angle droit a pour longueur le rayon du cercle et l’autre côté de l’angle droit a pour longueur le périmètre de la figure polygonale. Or cette figure est inscrite dans le cercle et, par convexité, son périmètre est donc inférieur au périmètre du cercle. La contradiction est obtenue puisque l’on a montré cette fois que l’aire polygonale est inférieure à T. On démontre l’impossibilité de l’inégalité S 麗 T de manière analogue en utilisant cette fois une dichotomie relative à un carré dans lequel le cercle est inscrit.

3^e temps: encadrement de la raison, réalisé au moyen d’un calcul algorithmique (cf. ALGORITHMIQUE, chap. 1) et faisant déjà intervenir des approximations. Archimède, partant de l’égalité S/R² = p/d procède par évaluation des longueurs des figures polygonales respectivement inscrites et circonscrites à chaque étape de la dichotomie. En termes modernes, la longueur a ⁿ du côté de la figure polygonale à n côtés fournit la longueur a ²ⁿ de la figure polygonale à 2n côtés par la formule:

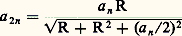Archimède énonce ce résultat en termes géométriques n’utilisant que les proportions, ce qui laisse à penser que leurs manipulations étaient raffinées et algébrisées. Mais, à chaque étape, il faut estimer une racine carrée; et cette approximation en nombres rationnels est donnée par Archimède sans aucune explication, soit qu’il considère ces approximations comme de pure routine, ce qui supposerait un fort courant numéricien, soit qu’il se réfère à un traité antérieur qui ne nous serait pas parvenu. En se limitant à 96 côtés, on obtient l’encadrement annoncé.

Il faut souligner que la méthode d’exhaustion mêle l’aspect théorique et l’aspect numérique, l’un s’appuyant sur l’autre. C’est un caractère de la mathématique grecque que ne possède pas la mathématique chinoise, bien que cette dernière parvienne à des estimations remarquables de 神 (cf. CHINE Sciences et techniques en Chine).

Il faut évoquer, ne serait-ce que rapidement, le contexte épistémologique de cette construction des raisons. La crise intellectuelle due à l’émergence des irrationnels a, en effet, suscité de profondes réflexions et une certaine concaténation des procédures mentales. D’abord, très vraisemblablement, se manifeste un doute fondamental sur les possibilités du raisonnement logico-déductif, puisque le sens commun était bafoué. Ce doute s’incarne dans les paradoxes de Zénon, dont le plus célèbre évoque Achille au pied léger qui jamais ne peut rattraper la tortue, puisque, chaque fois qu’Achille parcourt la moitié de l’espace qui le sépare de la tortue, l’animal a avancé quelque peu. On a trop insisté sur l’aspect lié au mouvement de ces paradoxes, alors qu’il s’agit de mettre en cause toute procédure liée à l’infini, aussi bien dans le continu que dans le discret. Zénon consacre une double contradiction avec l’emploi, dans un sens ou dans le sens opposé, d’hypothèses finitistes ou infinitistes sur le continu. Il y a contradiction à supposer que le temps, modèle du continu, est composé de grains discrets (non divisible à l’infini) alors que la longueur serait divisible à l’infini (sans atomes). Mais il y a aussi contradiction à supposer temps et longueurs atomisés, ou encore à les supposer divisibles à l’infini (continus au sens d’avant Eudoxe); cette dernière contradiction, voilée de nos jours, provient de l’emploi de raisonnements et de calculs valables pour le discret seulement ^{[cf. CONTINU ET DISCRET]}.

La résolution des paradoxes de Zénon s’effectue en deux temps. D’une part le calcul des séries qui apprend à sommer une famille infinie de quantités de plus en plus petites, d’autre part la théorie des cardinaux, due à Cantor, opposant «dénombrable» à «non dénombrable» et mettant en évidence les pièges d’un calcul prétendument numérique avec des nombres infinis (nombres transfinis). Eudoxe, Aristote, Spinoza ou Bergson, parmi d’autres, se pencheront sur le problème. Pour Eudoxe, le continu provient d’un donné divisible à l’infini (les grandeurs), se construit comme un modèle universel au terme d’une théorisation rigoureuse et peut être soumis à un certain calcul. Cependant, selon la conception platonicienne, puisqu’on part d’hypothèses et qu’on procède par déductions logiques, on ne peut parvenir à l’Idée pure; en particulier, les raisons ne bénéficient pas de toute la force opératoire du numérique discret. Euclide reprend toute la théorie des rapports pour envisager les propriétés des rationnels, ne se contentant pas d’appliquer le livre V. Pour Aristote, l’essence du continu est sa divisibilité à l’infini, ce qui résout tout un pan des paradoxes de Zénon mais laisse subsister une dernière contradiction. Aristote s’attache alors à distinguer l’infini virtuel de l’infini actuel, laissant la pensée mathématique opérer sur le premier seulement. Kant reprendra ces attitudes limitant le pouvoir de la raison par des antinomies (pour toutes ces questions, cf. INFINI MATHÉMATIQUE).

Avant d’en venir à d’autres aspects constitutifs des nombres réels, suivons les aventures de la théorie des proportions en sautant quelques siècles.

Les séries et les méthodes algorithmiques

Jusqu’au XVIII^e siècle, la méthode d’exhaustion, jointe à la théorie des proportions, exerce une fascination un peu désespérée dans la mesure où sa remarquable élégance s’accompagne d’une mise en œuvre presque spécifique à chaque cas, notamment dans la dichotomie algorithmique. Aussi l’apparition de nouvelles méthodes d’approximation des raisons est-elle reçue avec avidité, quand bien même la rigueur y perd son compte. Un tel nouveau calcul devient systématique au XVII^e siècle, avant même la construction du calcul infinitésimal (cf. CALCUL INFINITÉSIMAL - Histoire, CALCUL NUMÉRIQUE); il s’agit du calcul des séries, que bien des aspects rattachent à la méthode d’exhaustion.

L’aspect calculatoire de ces premières séries est essentiel. Il ne s’agit nullement d’une théorie de la convergence, mais d’un procédé algorithmique de calcul et chaque terme de la série est explicitement déduit de son prédécesseur par des opérations répertoriées. Ainsi, la série géométrique est envisagée du point de vue des proportions: chaque terme est à son successeur ce que le premier terme est au second, et la notation .... a : aq : aq ² : aq ³... sera employée jusqu’au XIX^e siècle. La somme des n premiers termes, est donnée par Euclide, et Viète, en 1593, donne pour q 麗 1 la somme infinie:

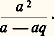Dans son monumental ouvrage, Opus geometricum (1647), Grégoire de Saint-Vincent montre que ce calcul résout le paradoxe de Zénon concernant Achille et la tortue. S. Stevin, avec la Disme, publiée en 1585, avait popularisé l’écriture décimale d’un nombre entier et d’un nombre rationnel (écriture illimitée mais périodique); pour une raison quelconque, le développement décimal est également la somme d’une série:

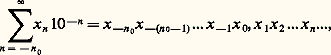les coefficients x ⁿ étant des chiffres, c’est-à-dire des entiers compris entre 0 et 9. On constate la double écriture des nombres décimaux: soit uniquement des 9 à partir d’un certain rang, soit uniquement des zéros à partir de ce même rang, mais en ajoutant une unité au rang précédent, ce qui se déduit de l’égalité:

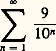La justification de la réciproque, à savoir que toute écriture décimale illimitée fournit un nombre, devra attendre le critère de Cauchy et, en fait, la construction des réels (cf. infra ).

D’autres calculs liés à l’infini font leur apparition à l’aube du XVII^e siècle. Viète, reprenant la méthode d’exhaustion en raffinant le processus algorithmique, obtient la raison comme produit infini:

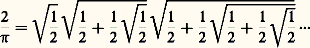De nombreux auteurs obtiennent pour ce nombre des approximations très précises; ainsi Ludolf van Ceulen donne-t-il en 1596 la valeur de 神 avec 35 décimales.

C’est la piste théorique tracée par Viète qui l’emporte peu à peu. Wallis, en 1655, donne le produit infini:

que lord Brounker transforme, pour obtenir:

Une expression semblable avait déjà été proposée par Bombelli en 1572 pour 連2; l’algébriste italien part de 連2 = 1 + 1 見 et vérifie 見 = 2 + 1 見 . Il écrit donc a priori une forme répétitive: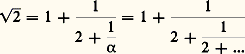

Cette théorie des fractions continues sera reprise et théorisée par Euler et Lagrange (cf. approximations DIOPHANTIENNES, chap. 1).

Au fil du temps, des fractions continues aux développements en série, de nombreuses techniques sont élaborées pour représenter les nombres réels et les mathématiciens prennent l’habitude de numériser le champ des raisons.

2. Les nombres comme solutions d’équations

Numérisation des raisons

Dans La mesure du cercle d’Archimède, nous avons déjà noté des approximations de raisons non rationnelles par des rapports rationnels. Ainsi 連a ² + b est-il approximé par a + b 2a (méthode dite de Héron, mais en fait beaucoup plus ancienne) ou par a + b 2a + 1. Dans le développement de ce type d’approximations, porteur de tout un courant numéricien, la géométrie et la théorie des proportions sont souvent requises à titre de justification ou d’illustration, mais on sent aussi la vigueur d’un courant de nature algébrique, traitant les opérations sur les nombres entiers ou rationnels comme un but en soi. Un vocabulaire particulier en résulte, qui parle par exemple d’additionner une circonférence à un diamètre, c’est-à-dire assimile pour le calcul une raison à un nombre, ou plutôt numérise le domaine des raisons.

Chez Diophante, ce langage est porté par un symbolisme notationnel qui est le rudiment des futures notations algébriques. Diophante insiste sur la résolution d’équations indéterminées du type:

où y est un entier, voire un nombre rationnel, et examine les solutions entières ou rationnelles en x . Mais il lui arrive de trouver une solution x non rationnelle et d’écrire «le nombre x se trouve non rationnel» (livre IV, problème 9, Arithmetica ), assimilant ainsi raison et nombre.

On trouve une attitude semblable chez les mathématiciens indiens ou arabes, avec quelquefois des remords de conscience, comme chez Omar Khayam (1048-1122), et des retours à la stricte obédience euclidienne. Partant les méthodes algébriques se systématisent, de pair avec les approximations numériques. Les mathématiciens chinois, sur lesquels l’influence euclidienne est virtuellement nulle, ont un traitement purement algébrique, qui ne fait pas de différence essentielle entre un nombre rationnel irréductible p /q , lorsque les nombres p et q sont assez grands, et un nombre irrationnel.

Les rencontres entre ce courant algébrique et le tradition euclidienne, plus ou moins bien transmise, ne sont pas rares. En voici un exemple typique, dû à Léonard de Pise (Leonardo Fibonacci). La méthode de l’alternance des signes permet de voir que l’équation polynomiale: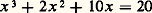

admet une seule racine x, d’ailleurs comprise entre 1 et 2. Léonard de Pise en donne une approximation très précise en prenant le développement sexagésimal de x jusqu’à l’ordre 6 (précision de l’ordre de 3.10^-11); mais ce calcul admirable n’est pas son but ultime. Il montre que la racine ne peut pas être rationnelle en prenant, à la manière euclidienne une forme irréductible p /q et en concluant, de p ³ = q (20q ² 漣 10pq ² 漣 2p ²q ), à la divisibilité impossible de p par q. Mais il poursuit, en démontrant que la racine ne peut pas être racine carrée d’un nombre rationnel, car l’écriture:

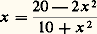montre que x lui-même serait rationnel. Enfin, il établit que x n’est d’aucune des formes de raisons irrationnelles classées par Euclide au livre X et qui reviennent à la forme:

Classification des nombres réels

Ainsi, la classification euclidienne, fondée sur la géométrie, est insuffisante pour les problèmes de résolution d’équations. On tient là l’embryon de la classification purement algébrique des nombres réels, qui remonte à Legendre (1752-1833). On appelle nombre algébrique toute solution d’une équation polynomiale à coefficients entiers (relatifs); ainsi 連2 est-il algébrique comme solution de x ² 漣 2 = 0. La racine étudiée par Fibonacci est aussi algébrique.

Par contraste, les autres nombres sont dits transcendants. Cette classification étonne car, à l’époque où elle fut donnée, il était impossible de fournir un seul exemple de nombre transcendant, bien que le candidat retenu par tous fût 神. C’est Liouville qui, en 1844, fournit le premier exemple de tels nombres en utilisant une propriété de mauvaise approximation des nombres transcendants par les nombres rationnels (cf. approximations DIOPHANTIENNES, chap. 3). Hermite, prouve en 1873, la transcendance de e et Lindemann, en 1882, celle de 神. Cantor, par comparaison des infinis, établit a priori l’existence de «beaucoup» de nombres transcendants (cf. nombres TRANSCENDANTS). Vers la même époque, Dedekind lance la théorie des nombres algébriques ^{[cf. NOMBRES (THÉORIE DES) - Nombres algébriques]}.

D’autres classifications des nombres provenaient de l’étude algébrique des équations polynomiales. Par exemple les nombres négatifs, solutions d’équations aussi simples que x + 7 = 0; leur introduction fut particulièrement difficile en Occident, car ces nombres ne pouvaient recevoir aucun statut dans le cadre des raisons euclidiennes définies à partir de grandeurs d’inspiration géométrique ou physique. En Chine, par contre, la pratique des équations avait conduit sans difficulté majeure à l’adoption de tels nombres.

De même les nombres complexes (cf. nombres COMPLEXES) furent introduits par les algébristes italiens du XVI^e siècle dans le cadre de la résolution des équations du troisième et du quatrième degré. La situation épistémologique de ces nombres était pire que celle des nombres négatifs puisque disparaissait toute la motivation eudoxienne à partir de l’ordre. La représentation géométrique des nombres complexes avec Wessel et Argand parut donner un statut à ces nombres. Argand, pourtant, insistait sur le fait que seules les considérations algébriques étaient requises et que la définition des nombres complexes étant opératoire, elle n’avait rien de plus surprenant que la définition de a ^-n = 1/a ⁿ , dont le seul but est la maintenance de la relation a ^n+m = a ⁿ a ^m pour tous les entiers relatifs. Ce point de vue des signes est celui qui est développé dans l’épistémologie génétique des mathématiques par Condillac au XVIII^e siècle: il n’y a pas d’êtres mathématiques, seulement des signes extensifs d’un domaine à l’autre par un jeu quasiment linguistique; l’algèbre est une langue et une langue est une méthode analytique. Et c’est bien cet aspect analytique qui avait guidé Descartes dans sa Géométrie (1637): rappelons que cette Géométrie se veut illustration et inspiration du Discours de la méthode .

3. Nombres et géométrie

La construction eudoxienne des raisons avait pris soin d’éviter trois écueils: l’utilisation d’arguments où interviendraient des procédures infinies, l’utilisation de procédures arithmétiques de calcul comme la multiplication des grandeurs, et, enfin, le recours à la géométrie. Pourtant, le modèle universel des raisons a été pensé comme réduit au modèle des seules raisons des longueurs géométriques et c’est la géométrie qui parut avoir primé sur la construction.

C’est bien dans ce cadre que Bombelli, dans la seconde moitié du XVI^e siècle (Algebra, 1572), après avoir choisi une unité de longueur, établit une correspondance biunivoque entre des longueurs et des raisons rapports de longueurs. Il peut alors définir géométriquement, à partir des longueurs, les opérations arithmétiques fondamentales, à savoir l’addition et la multiplication. La structuration opératoire du domaine des raisons, par cette référence explicite à l’espace, a donc pour fondement la géométrie. Ce point de vue de l’avantage de justifier le point de vue algébrique déjà évoqué et réconcilie des courants divergents. Cette fois c’est le continu, et non le discret, qui est opératoire. C’est ce même point de vue qui est exposé en quelques lignes au début de la Géométrie de Descartes, le modèle étant désormais étendu aux longueurs elles-mêmes (étant entendu que la longueur est une mesure, un rapport relativement à une unité). Par exemple, grâce à la quatrième proportionnelle, justifiée par le théorème de Thalès, le produit ab est la quatrième proportionnelle de la proportion a 1 = abb. Ce même point de vue avait permis à S. Stevin (1548-1620) de considérer comme d’un seul tenant les raisons tant rationnelles qu’irrationnelles, leur donnant désormais le nom générique de nombre. Une racine quelconque de nombre est nombre, de même que l’unité. Stevin dépasse, en fait, l’exposé cartésien, car il utilise, selon ses besoins, algèbre numérique ou géométrie, tandis que l’on sent Descartes tributaire de la géométrie. Il y a des racines «fausses» chez Descartes, mais aucun nombre «irrégulier», «absurde» ou «sourd» chez Stevin. C’est ce dernier point de vue qui sera moteur à la fin du XVII^e siècle, et c’est manifeste dans l’Algèbre de Rolle (1690). Pourtant, les manuels préfèrent le point de vue cartésien. On est en présence d’une scission entre l’enseignement, d’une part, et la mathématique en train de se faire d’autre part. Une situation analogue se retrouve enre 1900 et 1950, avec la théorie des ensembles et la topologie.

4. Nombres et analyse

Rôle des fonctions

Le langage des proportions, qui fait intervenir quatre éléments ou grandeurs, n’est guère propice à l’idée fonctionnelle, c’est-à-dire à la correspondance entre un élément et un autre. Aussi, en dehors des tables numériques à deux entrées, constate-t-on l’absence de représentations graphiques des variations de phénomène physique. Si l’on connaît un manuscrit arabe du XI^e siècle représentant la variation de la latitude des planètes en fonction de leur longitude, c’est à Nicolas Oresme (1325-1382) que l’on doit une représentation des variations en latitude (notre ordonnée) et longitude (notre abscisse). C’est une étape essentielle dans la compréhension du champ numérique, car elle assimile un point sur une droite à une raison, et ce bien avant Bombelli ou Descartes. Cette assimilation n’est pas «naïve», en ce sens qu’elle n’évacue pas la théorie des proportions par simple transfert analogique des propriétés des nombres entiers aux fractions, puis aux raisons quelconques, comme ce fut le cas dans le développement de l’algèbre polynomiale. En outre, on ne peut pas assimiler cette démarche à une géométrisation: le concept fonctionnel porte au-delà.

Ainsi, Oresme définit une fonction affine (qualitas uniformiter difformis ) au moyen d’une proportion qu’il exprime littéralement et que nous exprimerons en termes modernes, pour des points x ¹, x ², x ³ distincts mais quelconques: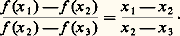

Oresme montre que la représentation graphique d’une telle fonction réalise un trapèze ABCD; il souligne aussitôt qu’il y a équivalence entre cette représentation en trapèze et la définition d’une fonction affine. Il en déduit qu’un changement d’échelle, c’est-à-dire un changement d’unité, donc un changement des raisons générant les points x ¹, x ², x ³ tout comme les points f (x ¹), f (x ²), f (x ³), ne modifie en rien la représentation en trapèze. L’invariance de la forme géométrique, conçue comme une aire car le calcul intégral est sous-jacent, permet une unité arbitraire, tant pour les abscisses que pour les ordonnées; en tant que telle, elle permet d’échapper aux limites des raisons. Du coup, des propriétés fonctionnelles vont immédiatement avoir une interprétation numérique.

Il ne faut pas croire, pourtant, que cette manipulation des proportions et des raisons soit si inadéquate au développement d’une physique mathématique. On peut soutenir que les raisons, qui réalisent une comparaison, ont une interprétation physique plus naturelle qu’un modèle abstrait, quoique universel, des nombres. Prenons l’exemple de la loi de la chute des corps pesants, magistralement établie par Galilée en 1638 au terme d’une analyse mathématique déductive confirmée par l’expérience (Discours sur deux nouvelles sciences ). Il faut montrer que le mouvement suivi par un corps pesant en chute libre est uniformément accéléré, c’est-à-dire que la vitesse suit les variations d’une fonction affine. Si tel est le cas, prenant une unié de temps t arbitraire, et des multiples entiers successifs de cette unité de temps, Galilée démontre mathématiquement que, si x (t ) est la distance parcourue au temps t par le corps (lâché sans vitesse initiale au temps t = 0), on a la proportion:

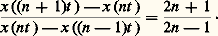L’unité de temps est mesurée expérimentalement par un volume d’eau constant s’écoulant d’un réservoir; le membre de gauche est la raison de l’accroissement de la distance parcourue d’une unité de temps à l’autre, le nombre de droite est la raison, de nombre à nombre, de deux entiers impairs successifs. Ainsi, l’aspect continu du mouvement uniformément accéléré a été réduit à du discontinu, du discret, grâce à la manipulation des proportions et à l’arbitraire de l’unité de temps. La vérification expérimentale confirme cette proportion et assure donc que le mouvement est uniformément accéléré.

La fonction logarithme

L’influence fonctionnelle déterminante sur la manipulation «logistique» des raisons est l’invention des logarithmes, au début du XVII^e siècle. Car c’est l’aspect opératoire qui est ici à l’œuvre, à partir de l’identité a ^n+m = a ⁿ 練 a ^m ; un produit d’un côté, une somme de l’autre. D’une part, la justification est géométrique, à partir de mouvements et de rapports de ces mouvements (des raisons, des礼塚礼﨟); d’autre part, la pratique calculatoire est arithmétique: à partir d’un nombre n, Napier détermine une puissance L telle que:

La liaison réalisée entre un礼塚礼﨟 et un 見福晴猪礼﨟 est un logarithme. Ce logarithme suit fondamentalement la relation fonctionnelle de transformation d’une somme en un produit: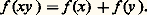

C’est à partir de cette relation fonctionnelle, vérifiée géométriquement – indépendamment de la création de Napier – pour des aires calculées sous l’hyperbole, que Grégoire de Saint-Vincent fera le lien avec la primitive de 1/x . Désormais, la numérisation du domaine des raisons passe aussi par le domaine fonctionnel et son développement, le calcul différentiel et intégral. Les méthodes se multiplient très vite (cf. CALCUL INFINITÉSIMAL - Histoire, CALCUL NUMÉRIQUE). C’est d’abord la mise en place systématique d’une nouvelle opération mathématique portant sur les raisons (les nombres réels positifs), l’exponentiation x ^y pour x et y positif. Le pas décisif est dû à Euler qui fait voir que:

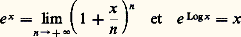et donne le développement en série de e^x qui permet l’extension au champ complexe (cf. EXPONENTIELLE ET LOGARITHME, chap. 4). Il en découle une profusion de résultats qui constituent l’analyse algébrique.

Retour aux raisons

Vers la fin du XVIII^e siècle, sous l’influence dominante de Lagrange, s’instaure une tentative de justification de ces méthodes fonctionnelles par une approche algébrique des développements infinis. C’est un échec, mais la recherche d’un fondement rigoureux est lancée qui, à travers Bolzano, Gauss et Cauchy donne un statut aux nombres réels (cf. BOLZANO, CAUCHY, GAUSS, fondements des MATHÉMATIQUES)

Dans son Cours d’analyse de 1821, Cauchy reprend à son compte la démarche de Bombelli et de Descartes de numérisation du champ des raisons à partir de la seule géométrie et énonce son critère de convergence d’une suite de nombres réels: une suite (x ⁿ ) converge si, pour tout 﨎 礪 0, il existe un entier N tel que pour tous m , n 閭 N, on ait |x ⁿ 漣 x ^m | 麗 﨎. Cauchy en démontre la nécessité à partir de sa définition de la limite, qui est la définition moderne; la suffisance est énoncée comme allant de soi. En 1817, Bolzano tente une telle démonstration et parvient au moins à démontrer l’unicité de la limite. La conscience d’une difficulté inhérente à la preuve du critère de Cauchy germait.

Le théorème des valeurs intermédiaires, qui affirme qu’une fonction f continue sur un intervalle [a , b ] telle que f (a )f (b ) 麗 0 doit s’annuler dans cet intervalle a joué un rôle moteur dans la caractérisation des nombres réels (cf. BOLZANO et infra, chap. 6).

Voici, en termes modernes, comment s’articule en substance la démonstration de Bolzano. Supposons f (a ) 麗 0 pour fixer les idées et considérons l’ensemble E de tous les x de [a , b ] tels que f (x ) 麗 0. Cet ensemble est non vide, majoré par b. S’il possède une borne supérieure c , il résulte facilement de la continuité que f (c ) = 0. Pour montrer que E possède une borne supérieure, Bolzano utilise une méthode de découpage dyadique.

Pour x ¹ 捻 E et x ² majorant de E, il introduit y ¹ = (x ¹ + x ²)²; ou bien y ¹ 捻 E et il prend le milieu de y ¹ et x ², ou bien y ¹ 殮 E et il prend le milieu de x ¹ et y ¹. Il renouvelle l’opération, déterminant ainsi successivement des nombres dont il est facile de montrer qu’ils satisfont au critère de Cauchy. Bolzano croit démontrer ce critère par la méthode des segments emboîtés, donc nous sommes très proches d’une démonstration correcte au sens moderne. Et pourtant nous tournons en rond, car la définition des nombres réels est encore indéterminée, trop vague pour assurer, autrement que par visualisation géométrique, l’existence d’un point ultime, limite d’une suite de Cauchy, ou d’un point limite commun à tous les segments emboîtés.

5. Construction de l’ensemble des nombres réels

Le critère de convergence d’une suite énoncé par Cauchy, comme le théorème des valeurs intermédiaires «prouvé» par Bolzano firent vite partie de la panoplie de travail de tout analyste. Mais ces théorèmes semblaient entachés de géométrisme, dérivant de la théorie des proportions que Descartes avait rattachée à la géométrie. Or, après la découverte des géométries non euclidiennes par Lobatchevski (1829), Bolyai (1832) et Riemann (1854), le géométrisme avait mauvaise presse.

Dedekind et l’ordre

L’approche de R. Dedekind ^{[cf. DEDEKIND (R.)]} est un retour à l’esprit de la construction eudoxienne. Eudoxe avait construit le modèle des raisons à partir seulement des grandeurs (le continu) et des entiers (le discret). Il utilisait à cet effet l’ordre comme règle d’extension (les raisons sont totalement ordonnées, comme les entiers ou les grandeurs). Dans Stetigkeit und irrationale Zahlen (1872), Dedekind construit les nombres réels à partir des rapports d’entiers – les nombres rationnels – en utilisant l’ordre comme règle à compléter. Voici en quoi consiste cette démarche.

Considérons avec Dedekind l’ensemble C de tous les nombres rationnels positifs x tels que x ² 閭 2. Il est clair que C est un ensemble minoré, c’est-à-dire: il existe un rationnel r , par exemple r = 1, tel que, pour x 捻 C on ait x 閭 r. Si r est un autre rationnel positif tel que r 麗 r , c’est encore un minorant de C. Existe-t-il, parmi les rationnels, un plus grand minorant, à savoir une borne inférieure de C ? La réponse est négative.

En effet, il suffit d’établir qu’une telle borne inférieure, disons m, si elle existait, vérifierait m ² = 2, équation impossible dans les nombres rationnels. Comme pour la méthode d’exhaustion, il convient, pour établir cette égalité, de raisonner par l’absurde. Supposons d’abord m ² 礪 2. Puisque m 礪 0, cherchons un rationnel y tel que y 礪 0, m 礪 y et (m 漣 y )² 閭 2. C’est possible: il suffit pour cela que y vérifie 0 麗 y 麗 d où d est le plus petit des deux nombres positifs (m ² 漣 2)/2m et m. Ainsi, m 漣 y est un élément de C strictement inférieur à m ; donc m n’est pas un minorant de C ni, a fortiori, une borne inférieure de C. Supposons d’autre part m ² 麗 2. Imposant à y les conditions 0 麗 y 麗 d , où d est le plus petit des deux nombres positifs 2 + m et (2 漣 m ²)/(2 + m ), on obtient un rationnel y tel que (m + y )² 麗 2, ainsi, m + y est un minorant de C qui dépasse m , en contradiction avec le fait que m soit borne inférieure.

De la même façon, si on désigne par C le complémentaire de C dans l’ensemble des nombres rationnels cet ensemble ne possède pas de borne supérieure rationnelle. Le couple (C,C ) est l’exemple d’une coupure, au sens de Dededkind.

On constate ainsi l’existence dans l’ensemble des nombres rationnels, de sous-ensembles non vides minorés et sans borne inférieure rationnelle (ou non vides, majorés, et sans borne supérieure). Cette constatation de manque est d’autant plus significative qu’elle traduit le manque de 連2, qui est précisément le nombre que l’on veut définir. L’idée est de compléter l’ensemble des nombres rationnels en ajoutant, avec préservation de l’ordre, des points supplémentaires de telle sorte que, dans le nouvel ensemble obtenu, tout sous-ensemble minoré admette une borne inférieure. La démarche de Dedekind est d’enrichir l’ensemble des nombres rationnels pour compenser une propriété manquante de ces nombres pris dans leur ensemble.

Techniquement parlant, Dedekind remarque que la relation d’ordre définie par l’inclusion sur l’ensemble de tous les sous-ensembles non vides d’un ensemble donné E possède la propriété de la borne inférieure. En effet, soit 遼 une famille non vide de sous-ensembles de E, famille minorée par un sous-ensemble B ø; cette minoration signifie que tout ensemble de la famille 遼 contient B. Alors, l’ensemble intersection des ensembles de la famille 遼 contient B, est un minorant de 遼 et c’est le plus grand des minorants, c’est-à-dire est la borne inférieure de 遼. De même, 遼 possède une borne supérieure réunion de tous les ensembles de 遼.

À partir de cette remarque, le construction de Dedekind s’organise aisément. Il appelle coupure (C, C ) de l’ensemble Q des nombres rationnels une partition de cet ensemble (c’est-à-dire C et C non vides, C 聆 C = Q et C 惡 C = ø) telle que tout rationnel de C dépasse strictement tout rationnel de C . Pour normaliser, on impose que, si C possède une borne inférieure dans Q, alors celle-ci appartient à C et non à C ; une telle coupure est dite section commençante fermée. On considère alors l’ensemble R de toutes les coupures muni de l’ordre de l’inclusion:

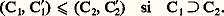Il est clair que cet ordre est total et possède la propriété recherchée: tout ensemble minoré non vide de R possède une borne inférieure. Il reste à montrer que Q est, de manière naturelle, un sous-ensemble totalement ordonné de R. Pour cela, il suffit d’identifier un nombre rationnel quelconque 見 à la coupure définie par C size=1^見, où:

Ainsi, Dedekind a construit de nouveaux éléments en les intercalant entre les nombres rationnels, sans perdre l’ordre et en gagnant la propriété de la borne inférieure. Il ne reste plus qu’à donner un nom aux éléments de R: ce sont les nombres réels. Ceux, parmi les nombres réels, qui ne sont pas identifiables à des rationnels, parce que la coupure C qui les définit n’a pas de borne inférieure, s’appellent les nombres irrationnels, tandis que les autres gardent le nom de nombres rationnels.

Cette construction de Dedekind fit scandale. D’une part, bien sûr, par les procédés mathématiques employés, dont la nouveauté laissait des doutes sur la validité. Cantor, avec la théorie des ensembles, habituera les mathématiciens à ces méthodes, ouvrant ainsi une orthodoxie nouvelle. D’autre part, le scandale tenait à la permanence du vocabulaire, repris de la tradition. Avait-on vraiment obtenu, au terme de la construction de Dedekind, des nombres identiques à ceux qu’on appelait irrationnels depuis l’Antiquité ? Une réponse positive ne pouvait qu’amener à douter de la construction euclidienne, enfin reconnue imparfaite.

Pourtant, en conservant la terminologie traditionnelle, Dedekind se conformait à la technique utilisée quelque cinquante ans plus tôt par Cauchy qui habillait les vieux mots de «limite» ou de «continuité» de ses propres définitions. Et cette attitude trouve sa justification dans le concept de définition tel qu’il est donné par Pascal dans le fragment De l’esprit géométrique et auquel il réservait l’expression de «définition de nom»: «Leur utilité et leur usage est d’éclaircir et d’abréger le discours, en exprimant, par le seul nom qu’on impose, ce qui ne pourrait se dire qu’en plusieurs termes; en sorte néanmoins que le nom imposé demeure dénué de tout autre sens, s’il en a, pour n’avoir plus que celui auquel on le destine uniquement.» En ce sens, on est fondé de dire que la coupure C construite avec x ² 閭 2 définit un nombre irrationnel.

Mais il y a problème à dire que cette même coupure définit l’irrationnel 連2, ce dernier étant connu comme «nombre» positif de carré égal à 2. Quelle que soit la signification donnée au mot nombre, il faut pouvoir parler de carré, donc de multiplication sur les nombres réels. Or rien dans la construction précédente n’a introduit une multiplication sur R. Autrement dit, pour reprendre l’analogie eudoxienne, nous n’avons pas numérisé R, de même qu’Eudoxe n’avait pas numérisé le domaine des raisons. Cette fois le chemin est tout tracé: il suffit d’étendre à l’ensemble totalement ordonné R la multiplication et l’addition définies sur les rationnels.

L’addition est facile à imaginer sur les coupures. Il suffit de poser: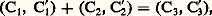

où C³ =x ¹ + x ²; x ¹ 捻 C¹, x ² 捻 C², et vérifier que (C³, C ³) est bien une coupure. On constate que, si les coupures proviennent de nombres rationnels 見 et 廓, on a:

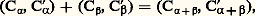où 見 + 廓 est bien la somme usuelle des rationnels 見 et 廓.

La multiplication est un peu plus délicate, car il faut tenir compte du changement d’ordre crée par la multiplication par un nombre négatif. Ainsi l’ensemble R des nombres réels est muni d’une addition et d’une multiplication, et ces opérations ont les propriétés usuelles. On établit en effet que R est un corps commutatif .

Comme sur Q, l’ordre et la structure de corps sont compatibles, en ce sens que x 諒 y implique x + z 諒 y + z , pour tout z de R et que x 閭 0 et y 閭 0 implique xy 閭 0. On dit qu’on a un corps totalement ordonné. Avec la propriété de la borne supérieure, on convient de dire que R est un corps ordonné complétement réticulé.

La théorie générale des espaces ordonnés généraux a digéré la construction de Dedekind et en fait un instrument de complétion (cf. infra chap. 6, Théorème 5 ). Il est en effet remarquable de constater que, si l’on considère l’ensemble de toutes les coupures sur R, on n’obtient rien d’autre que R. La procédure suivie par Dedekind est vraiment une complétion.

C’est bien ce caractère de complétion (corps complètement réticulé) qui, pour Dedekind, marque l’essence de la continuité et constitue son apport explicite par rapport à la construction eudoxienne. Le corps R est le modèle universel des rapports de grandeurs. En outre, la propriété de la borne supérieure mise en évidence permet une démonstration rigoureuse du théorème des valeurs intermédiaires de Bolzano, dont la seule faille était d’admettre cette propriété. De la même manière, la propriété de borne supérieure permet une définition irréprochable de la convergence d’une suite et établit aisément la convergence de toute suite croissante majorée. Avec la construction de Dedekind, toute l’analyse est assurée de ses fondements .

Cantor et les suites de Cauchy

Une autre construction des réels est due à G. Cantor et C. Meray (1872). Cette construction part aussi de la constatation d’une propriété qui manque aux rationnels: une suite de Cauchy de nombres rationnels ne converge pas nécessairement vers un nombre rationnel. Ainsi les approximations décimales successives de 連2 forment une suite de Cauchy dont la limite n’est pas rationnelle.

Cantor et Meray partent donc des nombres rationnels et définissent ce qu’ils appellent une suite fondamentale (x ⁿ ), que nous appelons aujourd’hui suite de Cauchy: Si pour tout rationnel 﨎 礪 0, il existe un entier N tel que:

Sur l’ensemble 倫 des suites fondamentales, Cantor établit plusieurs opérations:

– une addition: la suite (x ⁿ ) + (y ⁿ ) est la suite (x ⁿ + y ⁿ ), dont on vérifie aisément qu’elle est fondamentale;

– une multiplication: la suite (x ⁿ ) (y ⁿ ) est la suite (x ⁿ y ⁿ ), dont on vérifie facilement qu’elle est fondamentale;

– une relation d’ordre, notée 諒; (x ⁿ ) 諒 (y ⁿ ) s’il existe un entier N tel que, pour tout n 閭 N on ait y ⁿ 閭 x ⁿ .

Cantor, en fait, est plus précis. Lorsque (x ⁿ ) et (y ⁿ ) sont deux suites fondamentales, trois possibilités se présentent (qui s’excluent mutuellement, comme il est facile de le voir):

– ou bien il existe un nombre rationnel 見 礪 0 et il existe un entier N tel que, pour tout n 閭 N, on ait y ⁿ 漣 x ⁿ 閭 見;

– ou bien il existe un nombre rationnel 見 礪 0 et il existe un entier N tel que, pour tout n 閭 N, on ait 漣 見 閭 y ⁿ 漣 x ⁿ ;

– ou bien, pour tout nombre rationnel 見 礪 0, il existe un entier N tel que, pour tout n 閭 N, on ait |y ⁿ 漣 x ⁿ | 麗 見.

Dans le premier cas, on note que (x ⁿ ) 諒 (y ⁿ ) et, dans le deuxième, (x ⁿ ) 閭 (y ⁿ ). Dans le troisième cas, on devrait avoir (x ⁿ ) 諒 (y ⁿ ) et (x ⁿ ) 閭 (y ⁿ ). On conviendra, dans ce dernier cas, d’une égalité (x ⁿ ) = (y ⁿ ), c’est-à-dire, en fait, d’une relation d’équivalence sur l’ensemble 倫.

On vérifie que la classe d’équivalence de la somme (ou du produit) de deux suites fondamentales ne dépend que des classes d’équivalence des suites additionnées (ou multipliées).

La démarche de Cantor est plus prudente que celle de Dedekind. Il appelle nombre réel d’ordre 1 une classe d’équivalence de suites fondamentales. On vérifie facilement que l’ensemble R des nombres réels d’ordre 1 est ainsi structuré en corps comutatif totalement ordonné, et on note que Q est un sous-corps ordonné de R si on associe à tout rationnel x la classe de la suite fondamentale (x ⁿ = x ). On réservera l’appellation nombres réel d’ordre 0 aux rationnels.

Cantor appelle ensuite nombre réel d’ordre 2 une classe d’équivalence associée à une suite fondamentale de réels d’ordre 1. Plus généralement, on passe aux nombres réels d’ordre n. Le point essentiel est que l’ensemble des nombres réels d’ordre 2 ne se distingue pas, en tant qu’ensemble, de celui des nombres réels d’ordre 1. En langage moderne, R est complet c’est-à-dire qu’une suite fondamentale de nombres réels converge vers un nombre réel.

La démonstration est importante et nous montre l’introduction des outils essentiels de l’analyse. En effet, si (x ⁿ ) est une suite de nombres réels et x un nombre réel, on écrira x = lim x ⁿ si, pour tout 﨎 礪 0 il existe un entier N tel que, pour tout n 閭 N, on ait |x ⁿ 漣 x | 麗 﨎. (On peut prendre ici aussi bien 﨎 réel que seulement rationnel, sans changer la définition, la valeur absolue d’un réel étant facile à définir.)

Avec cette définition de la limite, on constate bien que si (x ⁿ ) est une suite fondamentale de nombres rationnels et x le nombre réel qui lui est associé, on a lim x ⁿ = x ; on énonce ce fait en disant que l’ensemble des rationnels est dense dans l’ensemble des nombres réels.

Il faut maintenant montrer que si (x ⁿ ) est une suite fondamentale de nombres réels, c’est-à-dire un nombre réel d’ordre 2, alors il existe un nombre réel unique x tel que lim x ⁿ = x ; autrement dit, R est complet. Chaque x ⁿ est défini par une classe d’équivalence de suites fondamentales de nombres réels d’ordre 0; soit (x ^{n ,m} ) un représentant où x ⁿ ,^m est rationnel. Soit 﨎 礪 0. Pour tout n fixé, il existe un entier N(n ) tel que, pour tout m 閭 N(n ), on ait |x ^{n ,m} 漣 x ⁿ | 麗 﨎/3. La suite de rationnels (x ^{n ,N(n)} ) est une suite fondamentale d’après la majoration, pour n assez grand,

cette suite définit donc un nombre réel x et on vérifie que lim x ⁿ = x .

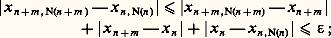On renvoie au chapitre 3 de l’article espaces MÉTRIQUES, pour l’exposé de cette méthode générale de complétion pour un espace métrique avec l’emploi de la méthode diagonale (due également à Cantor).

Un aspect épistémologique majeur de la construction de Dedekind et de celle de Cantor est que le point de départ est arithmétique, en ce sens qu’on n’utilise que la connaissance des nombres rationnels. Quelques années plus tard, aussi bien Cantor que Dedekind montrent que les mêmes méthodes ensemblistes, par passage au quotient pour des relations d’équivalence, permettent de construire Q à partir de l’ensemble N des entiers naturels, en passant par l’intermédiaire de l’ensemble Z des entiers relatifs. Ainsi, le continu, en l’occurrence R, se construit à partir du discret arithmétique. Cette construction porte un coup sérieux à la théorie kantienne du jugement synthétique selon laquelle le continu est une catégorie mentale a priori. Au contraire, la continuité est séparable de la notion d’espace et sert à spécifier, comme dans le cas de R, un espace continu.

Tout comme Dedekind, Cantor explicite donc la relation entre les nombres réels nouvellement construits et la droite de la géométrie usuelle. Sur une droite, graduée par la donnée d’un vecteur unité, on peut définir les points rationnels comme ceux dont l’abscisse est mesurée par un nombre rationnel. À tout point M de la droite on peut associer au moins une suite fondamentale (x ⁿ ), constituée de nombres rationnels, telle que les points d’abscisse x ⁿ se rapprochent de M lorsque n tend vers l’infini. Réciproquement, Cantor pose en axiome qu’à tout nombre réel (non rationnel) correspond un point de la droite ayant ce nombre comme abscisse. Cantor précise qu’il s’agit d’un axiome «parce qu’il est dans sa nature de ne pouvoir être démontré de façon générale». De fait, l’axiome en question se condense sous la forme dite des segments emboîtés: si (I ⁿ ) est une suite de segments emboîtés fermés non vides d’une droite, c’est-à-dire Iⁿ⁺¹ 說 Iⁿ , et si la longueur de Iⁿ (pour une graduation de la droite) tend vers 0, il existe un unique point M de la droite appartenant à tous les Iⁿ .

6. Axiomatisation et conséquences

L’axiomatisation de Hilbert

Une fois bien notée la propriété de complétion comme une propriété maximale (soit sous la forme de la borne supérieure comme chez Dedekind, soit sous la forme de la convergence des suites de Cauchy comme chez Cantor), Hilbert propose une approche axiomatique des nombres réels. Il introduit une famille de nombres, notés x, y , ... de sorte que cette famille constitue:

(a ) un corps commutatif pour les deux lois +, .,

(b ) un corps totalement ordonné,

(c ) un groupe ordonné archimédien pour la loi +, c’est-à-dire: quels que soient x 礪 0 et y 礪 0, il existe au moins un entier naturel n tel que:

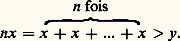(d ) un système qu’il ne soit pas possible d’agrandir en lui rajoutant des éléments de manière à obtenir un système vérifiant encore (a ), (b ) et (c ).

Il n’est pas difficile de montrer, en utilisant (d ), que, si un tel système existe, il est unique à un isomorphisme près, cette dernière expression signifiant que, si deux tels systèmes S¹ et S² sont donnés, il existe une bijection S¹S² qui est un homomorphisme de corps totalement ordonnés; S¹ et S² sont donc structurellement isomorphes. On aura donc loisir d’appeler ensemble des nombres réels tout système satisfaisant (a ), (b ), (c ), (d ).

Cependant, l’existence d’un tel système n’est pas évidente. Elle peut résulter des constructions précédentes de Cantor et Dedekind (ou d’autres constructions) comme nous allons le montrer. Toutefois la démarche de Hilbert était tout autre. Il s’agissait d’établir que les quatre conditions (a ), (b ), (c ), (d ) ne sont pas contradictoires, la non-contradiction d’une famille d’axiomes, pour autant qu’elle soit démontrée, assurant, selon le point de vue de Hilbert, l’existence d’un système d’objets satisfaisant les axiomes (cf. AXIOMATIQUE et chapitre 4 de HILBERT).

Passons maintenant à la démonstration de l’équivalence des constructions de Cantor et Dedekind et montrons qu’elles vérifient les quatre propriétés énoncées par Hilbert.

Caractérisation de R

Nous partons de la construction de Cantor, c’est-à-dire d’un corps totalement ordonné archimédien et complet R. Le théorème 1 indique que R est un modèle universel pour certaines propriétés.

Théorème 1. Soit G un groupe commutatif, totalement ordonné et archimédien. Il existe un homomorphisme strictement croissant de G dans R.

Si G est réduit à son élément neutre 0, le théorème est trivial. Soit a un élément fixé de G, supposé strictement positif. Soit x un élément quelconque de G. Pour tout entier n 閭 0, il existe un entier relatif k ⁿ tel que:

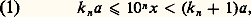puisque G est archimédien et que tout sous-ensemble majoré non vide d’entiers relatifs possède un plus grand élément.

On remarquera qu’une telle relation (1) est une autre façon, adaptée à la structure ordonnée, d’écrire la division euclidienne:

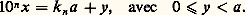Nous ne faisons donc que transposer en langage mathématique l’antique méthode numérique d’encadrements par sous-multiples successifs, renouant avec le courant numérique.

Comparons k ⁿ et k ⁿ⁺¹ :

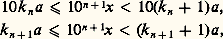donc:

Soit, puisque k ⁿ et k ⁿ⁺¹ sont des entiers, la double inégalité prévisible:

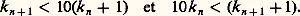
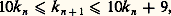et donc:

D’où, pour tout entier p 閭 1,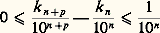

Par suite (k ⁿ /10ⁿ ) est une suite de Cauchy dans R (suite de nombres décimaux, donc rationnels): cette suite constitue les «approximations décimales» de x . Puisque, par hypothèse, R est complet, la suite (k ⁿ /10ⁿ ) converge vers un élément de R noté f (x ).

Nous venons d’exhiber une correspondance f : GR. Montrons que f est l’application cherchée. En effet:

– D’une part, f est une application strictement croissante. Soit x 麗 y , où x et y sont deux éléments de G. Notons k ⁿ (x ) et k ⁿ (y ) les entiers tels que:

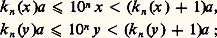d’où: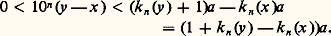

Puisque G est archimédien, il existe un entier N tel que 10^N (y 漣 x ) 礪 a. D’où, pour tout n 閭 N, on a:

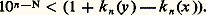Soit: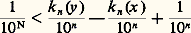

En passant à la limite en n :

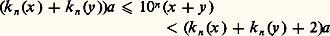et donc f (y ) 礪 f (x ) lorsque y 礪 x.

– D’autre part, f est un homomorphisme de G dans R. On écrit en effet les deux inégalités:

et:

soit: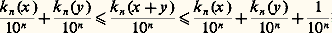

à la limite, on a:

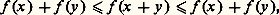c’est-à-dire l’égalité caractéristique d’un homomorphisme, ce qui termine la démonstration du théorème 1.

Remarquons que si, en outre, G est un anneau ordonné, on peut choisir convenablement a de sorte que la fonction précédente f : GR soit un homomorphisme d’anneau, c’est-à-dire vérifie aussi f (xy ) = f (x )f (y ); la démonstration est très voisine de la précédente.

Deux remarques en découlent. Puisque f est injectif et R commutatif, on a xy = yx , c’est-à-dire que l’anneau G est commutatif. Par ailleurs, la construction eudoxienne avec les raisons conduit facilement à un demi-corps totalement ordonné archimédien, en utilisant le terme «demi» pour marquer l’absence, chez Euclide, de raisons négatives. Le résultat précédent montre qu’un tel demi-corps doit être envisagé comme un sous-ensemble de R. C’est une autre façon de dire que la construction de R par Cantor est maximale par rapport à la construction d’Eudoxe.

Théorème 2. Ce théorème énonce que R satisfait les conditions (a ), (b ), (c ), (d ) de Hilbert.

En effet, tout système satisfaisant (a ), (b ), (c ) est isomorphe à un sous-ensemble de R. S’il possède également (d ), il s’identifie donc naturellement à R.

Le troisième théorème met en évidence l’unicité de la construction de Cantor.

Théorème 3. Tout corps totalement ordonné, archimédien et complet est isomorphe à R, donc unique, à un isomorphisme près.

La démonstration suit celle du théorème 1. Il suffit de montrer que l’application f : KR où K est un corps totalement ordonné, archimédien et complet, est surjective. Soit t un élément de R et les approximations décimales k ⁿ10^-n de t à 10^-n près. Considérons dans K la suite x ⁿ = k ⁿ 10^-n e , où e est l’unité de K; on a f (x ⁿ ) = k ⁿ 10^-n . On vérifie alors que la suite (x ⁿ ) est de Cauchy, donc converge vers x dans K; il en résulte f (x ) = t , ce qui prouve la surjectivité.

Le théorème suivant établit l’unicité de la construction de Dedekind.

Théorème 4. Tout groupe commutatif non réduit à l’élément neutre, divisible (c’est-à-dire que pour tout élément x et tout entier naturel n 閭 1, il existe y tel que ny = x ), archimédien et complètement réticulé, est isomorphe à R (pour sa structure de groupe ordonné).

Dans le cadre de la construction de Dedekind, on peut souhaiter un résultat d’unicité faisant surtout jouer la notion d’ordre, mais débarrassé de la structure algébrique. C’est l’objet du théorème 5.

Théorème 5. Soit D un ensemble totalement ordonné, ni majoré ni minoré, mais possédant la propriété de la borne supérieure pour tout ensemble non vide majoré et la propriété de la borne inférieure pour tout ensemble non vide minoré. Supposons qu’il existe un sous-ensemble dénombrable Q de D tel que, pour tout couple (x, y ) d’éléments de D avec x 麗 y , il existe un élément z de Q tel que x 麗 z 麗 y . Alors D est unique, à un isomorphisme d’ensemble ordonné près, et coïncide avec R.

La méthode de complétion de Cantor conduit, elle aussi, à des généralisations fécondes (complétion d’un espace métrique, cf. chapitre 3 de l’article espaces MÉTRIQUES). En analyse fonctionnelle, tout espace normé réel (ou complexe) est dense dans un espace de Banach réel (ou complexe), son complété.

Autres caractérisations

Le premier exemple est fondamental dans la théorie des algèbres normées (cf. algèbres NORMÉES). Le théorème de Gelfand-Mazur affirme que les seules algèbres de Banach qui soient des corps sont: le corps des nombres réels, celui des nombres complexes et celui des quaternions (à un isomorphisme de corps de Banach près). On peut éliminer les quaternions en requérant la commutativité. Pour éliminer les nombres complexes, on peut faire une remarque algébrique: ce corps possède des automorphismes autres que l’application identique, par exemple z 磻 , où 磻 est l’imaginaire conjugué (il y en a d’autres...). Au contraire, le seul automorphisme non nul de R est l’identité. En effet, soit f : RR tel que f (x + y ) = f (x ) + f (y ) et f (xy ) = f (x )f (y ), quels que soient x et y. La seconde relation fonctionnelle montre la positivité de f sur les réels positifs; d’après un résultat dû à Darboux, cette propriété entraîne, avec l’équation fonctionnelle f (x + y ) = f (x ) + f (y ), la continuité de f. Mais Cauchy a fourni toutes les solutions continues de cette équation fonctionnelle sous la forme f (x ) = ax , avec a 捻 R. Comme la seconde relation fournit a ² = a et que a 0, on a donc a = 1 et f (x ) = x. Ainsi, tout corps commutatif de Banach n’ayant que l’identité comme automorphisme est identique au corps des nombres réels.

Voici maintenant une caractérisation de R liée à la théorie des extensions algébriques ^{[cf. CORPS]}: l’ensemble R est un corps maximal parmi les corps totalement ordonnés, en ce sens qu’il n’existe pas d’extension algébrique totalement ordonnée de R différente de R. On peut montrer que cette caractérisation est équivalente à l’une des deux propriétés suivantes:

– L’extension algébrique R(i ), où i est solution de x ² + 1 = 0, est un corps algébriquement clos: c’est le corps des nombres complexes (théorème de d’Alembert-Gauss);

– Tout nombre positif est un carré et tout polynôme de degré impair admet une racine dans R.

Ces propriétés entraînent que les seuls polynômes irréductibles sur R sont les polynômes du premier degré et les polynômes du second degré de la forme a X² + b X + c , avec b ² 漣 4ac 麗 0.

Une construction algorithmique

Voici enfin une autre construction de R qui ne passe pas par le corps des nombres rationnels, mais utilise une définition algorithmique de la soustraction sur le développement décimal illimité (cf. CALCUL INFINITÉSIMAL – Calcul à une variable, chap. 1). C’est un retour à Bombelli et à Stevin.

Soit 倫 l’ensemble de toutes les suites (x ⁿ )ⁿ size=1^捻Z (doublement infinies, c’est-à-dire indexées par Z) où x ⁿ , pour chaque entier relatif n , est un chiffre, c’est-à-dire un entier compris entre 0 et 9. Définissons la retenue r (x , y ) de deux éléments x et y de 倫. C’est une suite doublement infinie (r ⁿ (xy )), où r ⁿ prend les seules valeurs 0 ou 1. On pose r ⁿ (x , y ) = 1 s’il existe un entier relatif m 礪 n tel que x ^m 麗 y ^m et x ^k 諒 y ^k pour tout entier k tel que n 麗 k 麗 m , et r ⁿ (x , y ) = 0 dans les autres cas. Remarquons que, s’il existe un entier relatif n ⁰ tel que x ⁿ = y ⁿ = 0 pour n 諒 n ⁰, alors r (x , y) correspond à la suite des retenues que l’on inscrites lorsqu’on applique l’algorithme de soustraction aux nombres réels X et Y: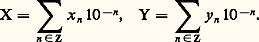

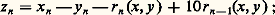À partir de deux éléments x et y de 倫, on définit alors z = (z ⁿ ) par la formule:

il est facile de vérifier que z 捻 倫. On pose alors x 省– y = z et on définit une addition sur 倫 en posant:

en désignant par 0 l’élément de R dont tous les termes sont nuls. Vérifiant que x 省 – (y 省 – t ) = t 省 – (y 省 – x ), on peut montrer que 倫 est un groupe commutatif pour l’addition ainsi définie. Toutefois 倫 est trop gros pour être convenablement ordonné. Considérons le sous-ensemble R de 倫 constitué des suites (x ⁿ ) pour lesquelles: ou bien il existe un entier relatif n ⁰ tel que x ⁿ = 0 pour n 諒 n ⁰ (on dit alors que l’on a un élément positif de 倫 et on désigne leur ensemble par R⁺), ou bien il existe n ⁰ tel que x ⁿ = 9 pour tout n 諒 n ⁰. On vérifie que R est un sous-groupe commutatif de (face=F0021 倫, +), mais surtout qu’en prenant comme relation d’ordre x 諒 y si y 漣 x 捻 R⁺, on obtient un groupe totalement ordonné. On montre aussi que R est archimédien, divisible et complètement réticulé. D’après le théorème 4, ce groupe est isomorphe à l’ensemble des nombres réels.

Cette construction est particulièrement adaptée aux calculs sur ordinateurs, car elle fournit un procédé algorithmique de calcul de l’addition de deux nombres écrits en développement décimal illimité.

Modèle non standard

Notre dernier exemple se réfère à l’analyse non standard. On se contentera ici d’une indication en renvoyant à l’article ANALYSE NON STANDARD. On va, cette fois, mettre de côté l’axiome d’Archimède pour rendre compte des phénomènes rencontrés par Leibniz au début du calcul infinitésimal.

Soit 輪 une famille non vide de sous-ensembles non vides de l’ensemble N des entiers naturels. On impose à cette famille les propriétés suivantes:

Une telle famille s’appelle un ultrafiltre (cf. théorie des MODÈLES). En dehors de l’exemple trivial où 輪 est la famille de tous les sous-ensembles de N contenant au moins un ensemble du type Aⁿ⁰ , l’existence des ultrafiltres utilise l’axiome du choix et leur description explicite est impossible. Quoi qu’il en soit, considérons l’ensemble 倫 de toutes les suites (x ⁿ ) de nombres réels. On définit alors sur 倫 la relation d’équivalence x 黎 y lorsque l’ensemble des entiers n tels que x ⁿ = y ⁿ appartient à 輪.

Considérons maintenant l’ensemble R, quotient de 倫 par la relation d’équivalence précédente. Il est facile de montrer que R est un corps totalement ordonné pour les lois déduites coordonnée à coordonnée de R à 倫 puis par passage canonique au quotient. En outre, il existe un homomorphisme injectif naturel du corps ordonné des nombres réels dans le corps R qui provient de l’identification d’un élément x de R à l’élément de 倫 dont, avant passage au quotient, toutes les coordonnées sont égales à x. En fait, R, beaucoup plus gros que R, est totalement ordonné, muni d’une valeur absolue, mais n’est pas archimédien. L’ensemble R, par rapport à R, possède des éléments qui, dans les calculs, jouent le rôle de quantités infiniment petites ou infiniment grandes. L’axiome d’Archimède excluait la considération de telles quantités. Dans R, appelé modèle non standard de R, le calcul algébrique habituel fournit les règles algorithmiques du calcul infinitésimal sur les quantités réelles. Par exemple, on dit qu’un élément z de R est un infiniment petit si, pour tout 﨎 礪 0, 﨎 捻 R, on a:

7. Rôle des nombres réels

Dans la vie quotidienne, l’ensemble R des nombres réels est le modèle auquel se rapporte toute mesure: une mesure par rapport à une unité de mesure choisie se traduit par un nombre réel.

Du point de vue mathématique, l’intérêt de l’ensemble des nombres réels est sa richesse, par profusion de structures imbriquées. Depuis la fin du XIX^e siècle, et tout au long du XX^e, les mathématiciens ont isolé des propriétés spécifiques de R leur permettant de définir et d’étudier des espaces abstraits satisfaisant ces seules propriétés.

D’abord, il y a la structure additive, qui conduit à la notion de groupe abélien, puis d’espace vectoriel réel, point de départ de l’algèbre linéaire. On définit aisément R², R³ et Rⁿ comme espaces vectoriels et ces espaces constituent le cadre idéal de la géométrie classique. Ainsi, on peut déduire toute la géométrie euclidienne de la construction de R et donc de l’ensemble des entiers naturels et de la théorie des ensembles (arithmétisation de la géométrie, cf. GÉOMÉTRIE).

Du point de vue de la théorie des ensembles, il y a la richesse de R en éléments. Cantor a montré que R est beaucoup plus «grand» que le corps Q des nombres rationnels (cf. supra et nombres TRANSCENDANTS, chap. 1): l’ensemble R a un cardinal non dénombrable, alors que Q est dénombrable. Le problème se pose aussitôt de savoir s’il existe un sous-ensemble E de R dont le cardinal soit strictement contenu entre le dénombrable et le cardinal de R, appelé puissance du continu. Cette question, qui tracassera Cantor toute sa vie ^{[cf. CANTOR (G.)]} a été résolue par P. J. Cohen en 1962; c’est un des résultats les plus brillants de la logique mathématique de l’après-guerre. Cohen a démontré que, sur la seule base de la théorie des ensembles, ce problème est indécidable; autrement dit, il n’est pas contradictoire avec la théorie des ensembles d’admettre l’existence d’un tel ensemble E, mais il n’est pas contradictoire non plus d’en refuser l’existence. Cette démonstration a donné naissance à toute une série de résultats indécidables relatifs à la théorie de la mesure et à la topologie de R, en liaison avec l’axiome du choix (problème de la mesure, problème de Souslin; cf. théorie axiomatique des ENSEMBLES, chap. 6).

La topologie de R, définie par Cantor à partir des intervalles ouverts, qui permet de donner un sens ensembliste à des notions comme les voisinages ou la continuité, est le point de départ de la topologie générale. Mais les nombres réels ont leur rôle spécifique à jouer en topologie générale, et Nicolas Bourbaki leur consacre le chapitre 9, intitulé «Utilisation des nombres réels en topologie générale» du livre III (Topologie générale) de ses Éléments. La notion d’écart, qui permet de définir une structure uniforme, se spécialise en la notion fondamentale de distance qui conduit à la théorie des espaces métriques (cf. espaces MÉTRIQUES). Dans ces espaces, le processus de complétion de Cantor s’applique et est au cœur de l’analyse fonctionnelle. En théorie des nombres, la complétion de Q pour les valeurs absolues p -adiques conduit aux nombres p- adiques (cf. théorie des NOMBRES - Nombres p -adiques).

La topologie de R est également étroitement liée à des questions de dénombrabilité. Tout ouvert de R est réunion dénombrable d’intervalles ouverts. Peut-on obtenir R comme réunion d’ensembles ne contenant pas d’intervalle (un tel ensemble est dit rare)? R. Baire a démontré qu’un ouvert non vide de R ne peut pas s’obtenir comme réunion dénombrable d’ensembles rares. Cette propriété caractérise les espaces de Baire, dont les espaces métriques complets constituent un important exemple (cf. espaces MÉTRIQUES, chap. 4, où l’on trouvera des références précises à l’analyse fonctionnelle).

Encyclopédie Universelle. 2012.